

The orthocenter of $\Delta ABC$ coincides with the circumcenter of $\Delta A'B'C'$ whose sides are parallel to those of $\Delta ABC$ and pass through the vertices of the latter. ConsiderD ABC with altitudes By definition of an altitude of a triangle, is perpendicular to, is perpendicular to and is perpendicular to. The foot of an altitude also has interesting properties. For example, due to the mirror property the orthic triangle solves Fagnano's Problem. I have collected several proofs of the concurrency of the altitudes, but of course the altitudes have plenty of other properties not mentioned below. Let's observe that, if $H$ is the orthocenter of $\Delta ABC$, then $A$ is the orthocenter of $\Delta BCH,$ while $B$ and $C$ are the orthocenters of triangles $ACH$ and $ABH,$ respectively.
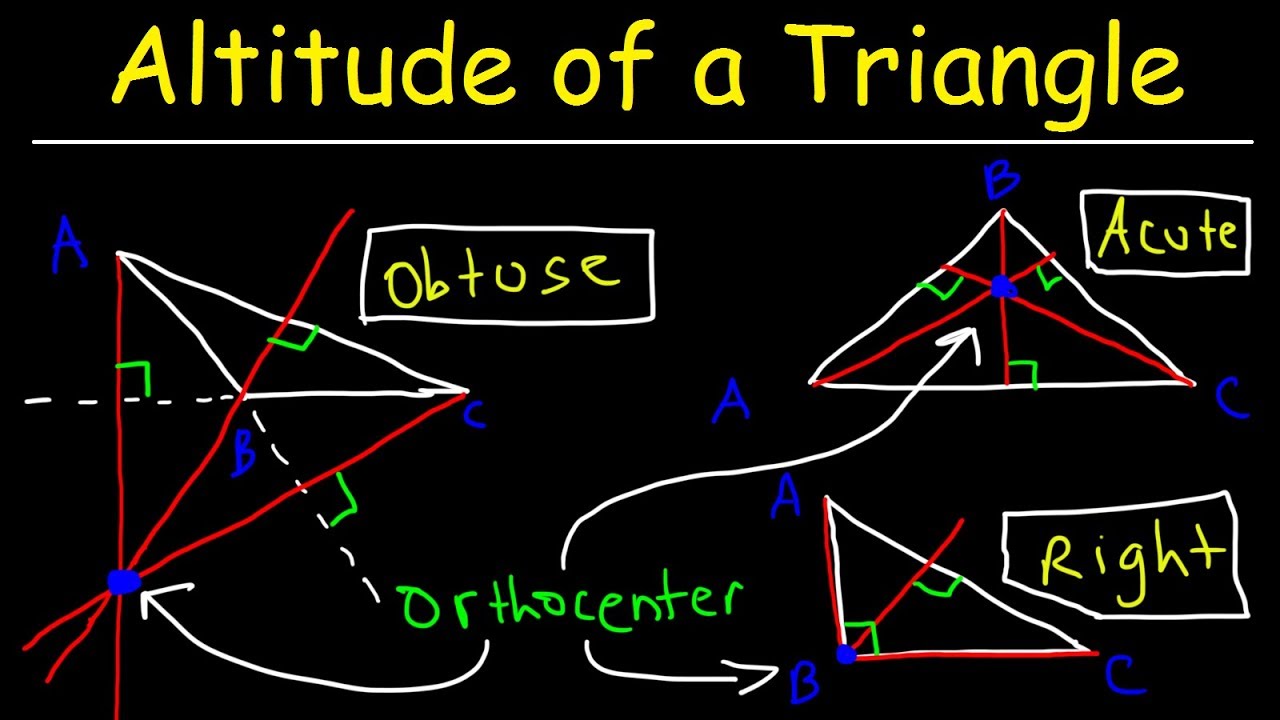
Consider a right angled triangle, A B C which is right angled at C. It is listed below, but appears on a separate page along with historical remarks. Right Triangle Altitude Theorem: This theorem describes the relationship between altitude drawn on the hypotenuse from vertex of the right angle and the segments into which hypotenuse is divided by altitude. The earliest known proof was given by William Chapple (1718-1781). For scalene or equilateral triangle, any side can be. The timing of the first proof is still an open question it is believed, though, that even the great Gauss saw it necessary to prove the fact. Base meaning bottom, it refers to any side of a triangle, which is perpendicular to its height or altitude. But this would be how you draw from Dick Abad.This is a matter of real wonderment that the fact of the concurrency of altitudes is not mentioned in either Euclid's Elements or subsequent writings of the Greek scholars. Sectors should pass about if you notice all three pumpernickel, abide sectors cross at the same point. But this side, the particle by sectors should pass somewhere along this line that about and then the last side, the property goodbye. Also, known as the height of the triangle, the altitude makes a right-angle triangle with the base. For a triangle: a line at right angles to a side that goes through the opposite corner. The altitude of a triangle is the perpendicular drawn from the vertex of the triangle to the opposite side. And so, without any tools or anything like that, we're gonna estimate about where the vertical bisected will parts for this side of the political divide sector will pass about right there. Altitude (geometry) Generally: another word for height. Uh, and what we'll do is would will draw the public provides sector of each individual side. This would be an example of this gaming triangle. So what scaling triangle is is a triangle that has no congruent side. Description of Geometric Altitude for EGPWS 03/18/99 2 Geometric Altitude Geometric Altitude is a computed aircraft altitude designed to help ensure optimal operation of the EGPWS Terrain Awareness and Display functions through all phases of flight and atmospheric conditions. So we'll go ahead and draw a scaling triangle. Um, and it is perpendicular to that that launched. The line segment that means it passes through the middle. The altitude of a triangle is the perpendicular line segment drawn from the vertex of the triangle to the side opposite to it. Instead, the altitude intersects the projection of the opposite side. Since AD BC, product of slopes of AD and BC is equal to -1. As the picture below shows, sometimes the altitude does not directly meet the opposite side of the triangle. The line segments AD, BE and CF are called altitudes of the triangle ABC. So first of all, well, uh, we have her here is a proper tickled by sector and red it by sex. Definition: an altitude is a segment from the vertex of a triangle to the opposite side and it must be perpendicular to that segment (called the base). So what we'll be doing is the particular by sector of three sides of a scathing triangle.


 0 kommentar(er)
0 kommentar(er)
