

If we now rotate our line ever so slightly, how do we know that it does cross the line S after this rotation? In practice, we are always dealing with limited segments of straight lines, and cannot observe the whole of the straight line. Let there be a straight line through point P which is parallel to another line S. Though it seems intuitively true, there was no way of confirming it experimentally. Euclid and many of his followers had misgivings about this Parallel Postulate. Remember that lines are parallel if they lie in a common plane and never cross each other.
Euclid, who worked in Alexandria around 300 BC (practically nothing else is known about his life), developed a system of geometry which is still part of our mathematics curricula.
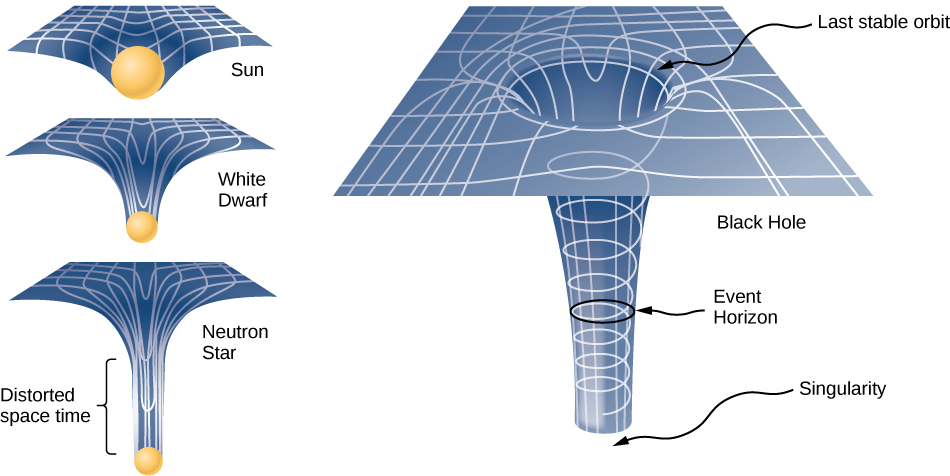
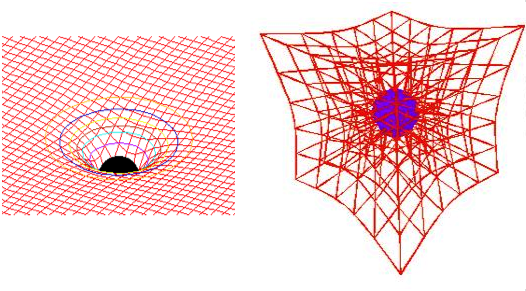
In fact, in the Special Theory of Relativity the spatial part of the four-dimensional space-time is flat (Euclidean). Our ordinary view of space is such that it resembles Euclidean geometry.


 0 kommentar(er)
0 kommentar(er)
